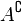PERIODO I: LÓGICA Y CONJUNTOS

 

ACTIVIDAD VIRTUAL N°1 GRADOS 6° 1, 2, 3 Y 4

(SEMANA DEL 15 -19  FEBRERO)
 
1) Ver el siguiente video:
 
 
2)Resolver el siguiente test en Educaplay:
 

www.educaplay.com/es/recursoseducativos/2264182/matematicas_6___proposiciones.htm

 

MUCHOS EXITOS EN ESTE PERIODO

 

Visita el blog https://javieramath6.blogspot.com

 

UNIDAD 1: LOGICA Y CONJUNTOS

 

CONJUNTOS  

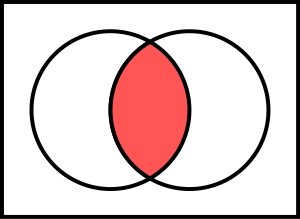
DIAGRAMAS DE VENN

Diagrama de Venn que muestra un conjunto A contenido en otro conjunto U y su complemento A^\complement

  Se entiende por conjunto un grupo de elementos con una o más características comunes. Por ejemplo:

A = El conjunto de los colores del arcoíris

B = {1, 3, 5, 7, 9}

Los conjuntos se representan por letras mayúsculas y sus elementos se encierran en llaves y se separan por comas.

Los conjuntos también suelen representarse mediante líneas cerradas en cuyo interior ubicamos los elementos del conjunto simbolizados por puntos. Estos son los denominados Diagramas de Venn:

 En los diagramas de Venn hay que tener en cuenta que: * Los elementos que no pertenecen al conjunto se representan por puntos exteriores a la curva.* Ningún punto se representa sobre la curva.

 

CONJUNTO VACIO

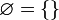Existe además, un único conjunto que no tiene elementos, al que se le llama conjunto vacío y que se denota por  \varnothing, esto es:  \varnothing = \{\}.

 

 

 

RELACIONES DE PERTENENCIA E INCLUSIÓN

Dado el conjunto A = {1,2,3,5,8}, observamos que 1 pertenece al conjunto A, por ser uno de sus elementos. Se denota como 1EA. en cambio, 6 no pertenece al conjunto A, se denota 6 /E A.

Entre elementos y conjuntos siempre se puede establecer una relación que llamamos relación de pertenencia.

Dados los conjuntos A = {a,b,c} y B = {a,b,c,d,e}, observemos que:

Se cumple que todos los elementos de E pertenecen también a F.

Luego el conjunto E se dice que está incluido en F, esto se denota como E C F.

Un conjunto A se dice que es subconjunto de otro B, si cada elemento de A es también elemento de B, y se denota A\subseteq B.

 Archivo:Venn A subset B.png

Diagrama de Venn que muestra que E Í F.

Cuando un conjunto A no está incluido en otro conjunto B, esto se denota como A /C B.

 

 OPERACIONES ENTRE CONJUNTOS

UNIÓN DE CONJUNTOS ∪

Para cada par de conjuntos A y B existe un conjunto unión de los dos, que se denota como A\cup B el cual contiene todos los elementos de A y de B.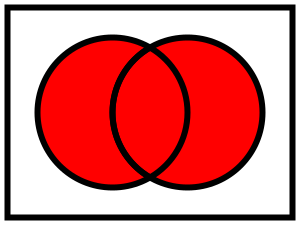 

 

A\cup B\equiv\{x:x\in A\text{ o }x\in B\}

 

Esto siginifica que x∈A∪B si y sólo si x∈A ó x∈B.

 

Diagrama de Venn que ilustra A\cup B

 

INTERSECCIÓN DE CONJUNTOS ∩

Los elementos comunes a A y B forman un conjunto denominado intersección de A y B, representado por A\cap B . Es decir, A\cap B es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B:

 

A\cap B \equiv \{x:x\in A\text{ y }x\in B\}

 

Esto siginifica que x∈A∩B si y sólo si x∈A y x∈B.

Diagrama de Venn que ilustra A\cap B

 Ejemplo: Dados los conjuntos U = {1,2,3,4,5,6,7,8}, A = {1,2,3,4} y B = {1,3,7} hallemos AUB, y el diagrama de Venn de los conjuntos indicando su intersección:

 

A\cup B= {1,2,3,4,7}   

A\cap B = {1,3}

__________________________________________________________________________________________________________________________

 

VER LOS SIGUIENTES VIDEOS COMO MATERIAL DE APOYO: